Make a Cheap Scaling
Make a Cheap Scaling: A Self-Cascade Diffusion Model for Higher-Resolution Adaptation
Abstract
- current problem: Diffusion models encounter challenges due to single-scale training data.
- solution:
- This paper proposes a novel self-cascade diffusion model that leverages the knowledge gained from a well-trained low-resolution image/video generation model, enabling rapid adaptation to higher-resolution generation.
- Building on this, we employ the pivot replacement strategy to facilitate a tuning-free version by progressively leveraging reliable semantic guidance derived from the low-resolution model.
- We further propose to integrate a sequence of learnable multiscale up-sampler modules for a tuning version capable of efficiently learning structural details at a new scale from a small amount of newly acquired high-resolution training data.
- Compared to full fine-tuning, our approach achieves a 5 × training speed-up and requires only 0.002M tuning parameters.
Introduction
Ways of scale up resolution
training: To scale up SD models to high-resolution content generation, a commonly employed approach is progressive training. i.e., training the SD model with lower-resolution images before fine-tuning with higher-resolution images. However, even a well-trained diffusion model for low-resolution images demands extensive fine-tuning and computational resources when transferring to a high-resolution domain due to its large size of model parameters. For instance:
SD 2.1 [7] requires \(550k\) steps of training at resolution \(256^2\) before fine-tuning with \(>1000k\) steps at resolution \(512^2\) to enable \(512^2\) image synthesis.
-
Attempted to utilize LORA [18] as additional parameters for fine-tuning, However, this approach is not specifically designed for scale adaptation and still requires a substantial number of tuning steps.
tuning-free methods:
-
Explored SD adaptation for variable-sized image generation using attention entropy
-
Utilized dilated convolution to enlarge the receptive field of convolutional layers and adapt to new resolution generation
-
Proposal
In this paper, we present a novel self-cascade diffusion model that harnesses the rich knowledge gained from a well-trained low-resolution generation model to enable rapid adaptation to higher-resolution generation.
- Our approach begins with the introduction of a tuning-free version, which utilizes a pivot replacement strategy to enforce the synthesis of detailed structures at a new scale by injecting reliable semantic guidance derived from the low-resolution model.
- Building on this baseline, we further propose time-aware feature up-sampling modules as plugins to a base low-resolution model to conduct a tuning version.
- To enhance the robustness of scale adaptation while preserving the model’s original composition and generation capabilities, we fine-tune the plug-and-play and lightweight up-sampling modules at different feature levels, using a small amount of acquired high-quality data with a few tuning steps.
The proposed up-sampler modules can be flexibly plugged into any pre-trained SD-based models, including both image and video generation models. Compared to full fine-tuning, our approach offers a training speed-up of more than 5 times and requires only 0.002 M trainable parameters. Extensive experiments demonstrated that our proposed method can rapidly adapt to higher-resolution image and video synthesis with just \(10 k\) fine-tuning steps and virtually no additional inference time.
Our main contributions are summarized as follows:
- We propose a novel self-cascade diffusion model for fast-scale adaptation to higher resolution generation, by cyclically re-utilizing the low-resolution diffusion model. Based on that, we employ a pivot replacement strategy to enable a tuning-free version as the baseline.
- We further construct a series of plug-and-play, learnable time-aware feature up-sampler modules to incorporate knowledge from a few high-quality images for fine-tuning. This approach achieves a \(5 \times\) training speed-up compared to full fine-tuning and requires only 0.002 M learnable parameters.
- Comprehensive experimental results on image and video synthesis demonstrate that the proposed method attains state-of-the-art performance in both tuning-free and tuning settings across various scale adaptations.
Related Work
High-resolution synthesis and adaptation. prior work can be broadly categorized into three main approaches:
Training from scratch: cost a significant amount of training data at high resolutions
- cascaded models: Cascade diffusion models employ an initial diffusion model to generate lower-resolution data, followed by a series of super-resolution diffusion models to successively up-sample it.
- end-to-end models: End-to-end methods learn a diffusion model and directly generate high-resolution images in one stage. i.e., sdxl.
Fine-tuning: Parameter-efficient tuning is an intuitive solution for higher-resolution adaptation
Tuning-free:
Methodology
Self-Cascade Diffusion Model (tunning free)
Scale decomposition
We aim to reuse the rich knowledge from the well-trained low-resolution model and only learn the low-level details at a new scale. We intuitively define a scale decomposition to decompose the whole scale adaptation \(\mathbb{R}^d \rightarrow \mathbb{R}^{d_R}\) into multiple progressive adaptation processes such that \(d=d_0<d_1 \ldots<d_R\) where \(R=\left\lceil\log _4 d_R / d\right\rceil\).
We first progressively synthesize a low-resolution image (latent code) \(z^{r-1}\) and then utilize it as the pivot guidance to synthesize the higher resolution result \(z^r\) in the next stage, where the reverse process of the self-cascade diffusion model can be extended by Eq. (3) for each \(z^r, r=1, \ldots, R\) as follows: \[ p_\theta\left(z_{0: T}^r \mid c, z_0^{r-1}\right)=p\left(z_T^r\right) \prod_{t=1}^T p_\theta\left(z_{t-1}^r \mid z_t^r, c, z_0^{r-1}\right) \] where the reverse transition \(p_\theta\left(z_{t-1}^r \mid z_t^r, c, z_0^{r-1}\right)\) not only conditions on denoising step \(t\) and text embedding \(c\), but also on lower-resolution latent code \(z_0^{r-1}\) generated in the last stage. Different from previous works, e.g., [16], LAVIE [35], and SHOW-1 [39] where \(p_\theta\) in Eq. 9 is implemented by a new super-resolution model, we cyclically re-utilize the base low-resolution synthesis model to inherit the prior knowledge of the base model thus improve the efficiency.
Pivot replacement
The information capacity gap between \(z^r\) and \(z^{r-1}\) is not significant, especially in the presence of noise (intermediate step of diffusion). Consequently, we assume that \(p\left(z_K^r \mid z_0^{r-1}\right)\) can be considered as the proxy for \(p\left(z_K^r \mid z_0^r\right)\) to manually set the initial diffusion state for current adaptation stage \(\mathbb{R}^{d_{r-1}} \rightarrow \mathbb{R}^{d_r}\), where \(K<T\) is an intermediate step. Specifically, let \(\phi\) denote a deterministic resize interpolation function (i.e., bilinear interpolation) to up-sample from scale \(d_{r-1}\) to \(d_r\). We up-sample the generated lower-resolution image \(z_0^{r-1}\) from last stage into \(\phi\left(z_0^{r-1}\right)\) to maintain dimensionality. Then we can diffuse it by \(K\) steps and use it to replace \(z_K^r\) as follows: \[ z_K^r \sim \mathcal{N}\left(\sqrt{\bar{\alpha}_K} \phi\left(z_0^{r-1}\right), \sqrt{1-\bar{\alpha}_K} \mathbf{I}\right) . \] Regarding \(z_K^r\) as the initial state for the current stage and conduct denoising with \(K \rightarrow 0\) steps as Eq. (3) to generate the \(z_0^r\), which is the generated higher-resolution image in the current stage.
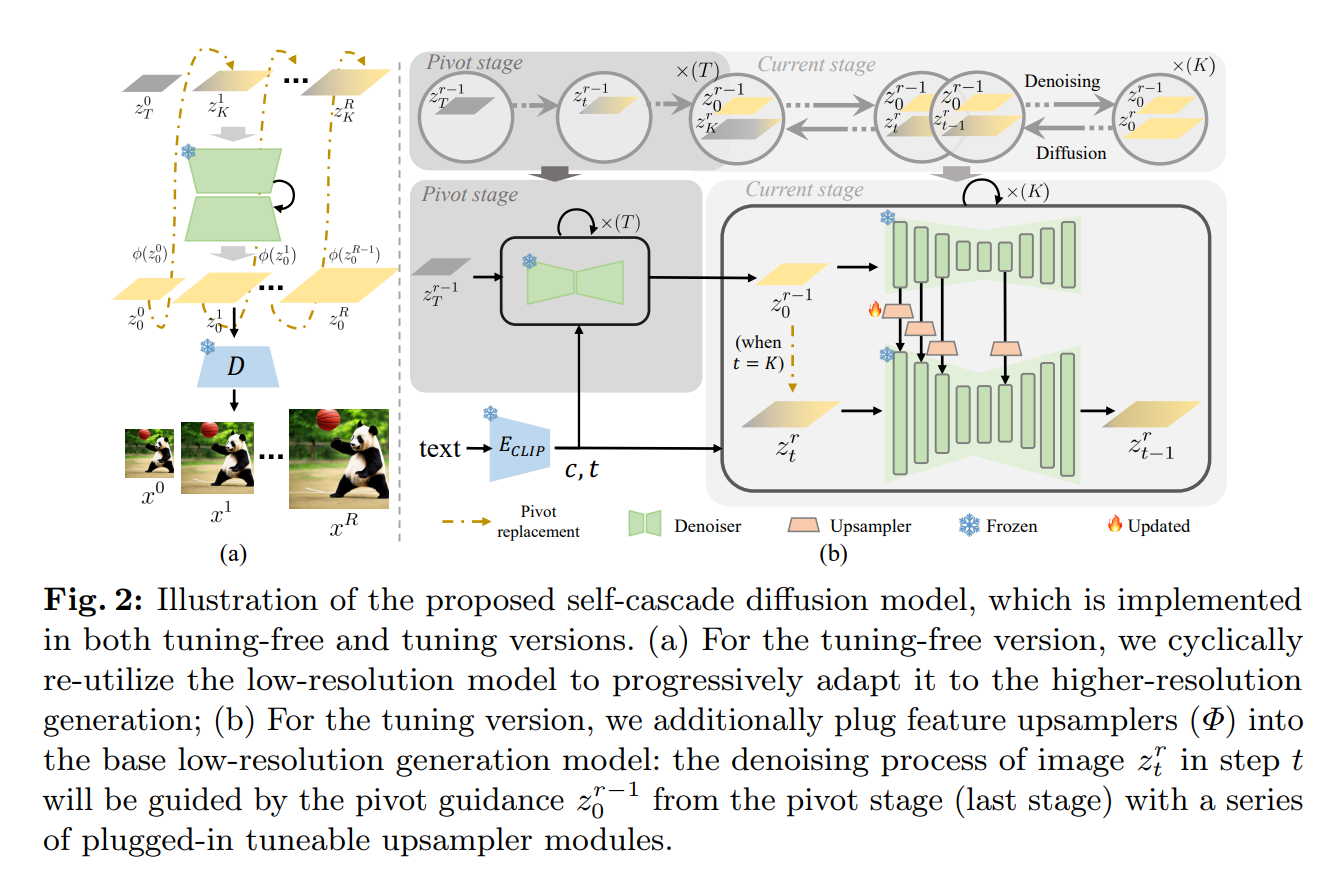
Feature Up-sampler Tuning (tunning version)
By inserting very lightweight time-aware feature upsamplers as illustrated in Fig. 2(b). The proposed upsamplers can be plugged into any diffusion-based synthesis methods. The detailed tuning and inference processes of our tuning version self-cascade diffusion model are in Algorithm 1 and 2 , respectively. Note that by omitting the tuning process and solely executing the inference step in Algorithm 2, it turns into our tuning-free version.
Specifically, given an intermediate \(z_t^r\) in step \(t\) and the pivot guidance \(z_0^{r-1}\) from the last stage, we can achieve corresponding intermediate multi-scale feature groups \(h_t^r\) and \(h_0^{r-1}\) via the pre-trained UNet denoiser \(\epsilon_\theta\), respectively, as follows:
\[ \begin{aligned} h_0^{r-1} & =\left\{h_{1,0}^{r-1}, h_{2,0}^{r-1}, \ldots, h_{N, 0}^{r-1}\right\} \\ h_t^r & =\left\{h_{1, t}^r, h_{2, t}^r, \ldots, h_{N, t}^r\right\} \end{aligned} \]
where \(N\) represents the number of features within each feature group and the details are included in the supplementary. In short, inspired by the recent work [27] that investigated the impact of various components in the UNet architecture on synthesis performance, we choose to use skip features as a feature group. These features have a negligible effect on the quality of the generated images while still providing semantic guidance. We define a series of time-aware feature upsamplers \(\Phi=\left\{\phi_1, \phi_2, \ldots, \phi_N\right\}\) to up-sample and transform pivot features at each corresponding scale. During the diffusion generation process, the focus shifts from high-level semantics to low-level detailed structures as the signal-to-noise ratio progressively increases as noise is gradually removed. Consequently, we propose that the learned up-sampler transformation should be adaptive to different time steps. The up-sampled features \(\phi_n\left(h_{n, 0}^{r-1}, t\right)\) is then added to original features \(h_{n, t}^r\) at each scale:
\[ \hat{h}_{n, t}^r=h_{n, t}^r+\phi_n\left(h_{n, 0}^{r-1}, t\right), \quad n \in\{1, \ldots, N\} . \]
Optimization details. For each training iteration for scale adaptation \(\mathbb{R}^{d_{r-1}} \rightarrow\) \(\mathbb{R}^{d_r}\), we first randomly sample a step index \(t \in(0, K]\). The corresponding optimization process can be defined as the following formulation:
\[ \mathcal{L}=\mathbb{E}_{z_t^r, z_0^{r-1}, t, c, \epsilon, t}\left(\left\|\epsilon-\tilde{\epsilon}_{\theta, \theta_{\Phi}}\left(z_t^r, t, c, z_0^{r-1}\right)\right\|^2\right) \] where \(\theta_{\Phi}\) denotes the trainable parameters of the plugged-in upsamplers and \(\theta\) denotes the frozen parameters of pre-trained diffusion denoiser. Each up-sampler is simple and lightweight, consisting of one bilinear up-sampling operation and two residual blocks. In all experiments, we set \(N=4\), resulting in a total of 0.002 M trainable parameters. Therefore, the proposed tuning self-cascade diffusion model requires only a few tuning steps (e.g., \(10 k\) ) and the collection of a small amount of higher-resolution new data.
