FreeScale

Posted on 2024-12-31 Edited on 2025-11-26 In notes , Diffusion , SR Disqus:

FreeScale: Unleashing the Resolution of Diffusion Models via Tuning-Free Scale Fusion

Abstract

Background: Diffusion models trained at limited resolutions makes them difficult to generate high-resolution images. Recent efforts have explored tuning-free strategies to exhibit the untapped potential higher-resolution visual generation of pre-trained models.
Problem: The key obstacle lies in the inevitable increase in high-frequency information when the model generates visual content exceeding its training resolution, leading to undesirable repetitive patterns deriving from the accumulated errors.
Solution:
- We propose FreeScale, a tuning-free inference paradigm to enable higher-resolution visual generation via scale fusion
- Specifically, FreeScale processes information from different receptive scales and then fuses it by extracting desired frequency components
- Notably, compared with previous best-performing methods, FreeScale unlocks the generation of 8k-resolution images for the first time.

Introduction

Diffusion Model Train Resolution
- SD1.5: \(512^2\)
- SDXL: \(1024^2\)
ScaleCrafter [18]
Cause: limited convolutional receptive field
Solution: uses dilated convolutional layers
Limit: local repetition

Exclude DiT for Cost: Since the DiT structure models often take up more memory, achieving high-resolution generation on a single GPU is difficult even in the inference phase. Therefore, we still use the U-Net structure models in this work. We chose SDXL [36] as our pre-trained image model, and VideoCrafter2 [10] as our pre-trained video model.

Training/tuning methods with high-resolution data and large models
Tuning-free methods without any additional data requirement

Methodology

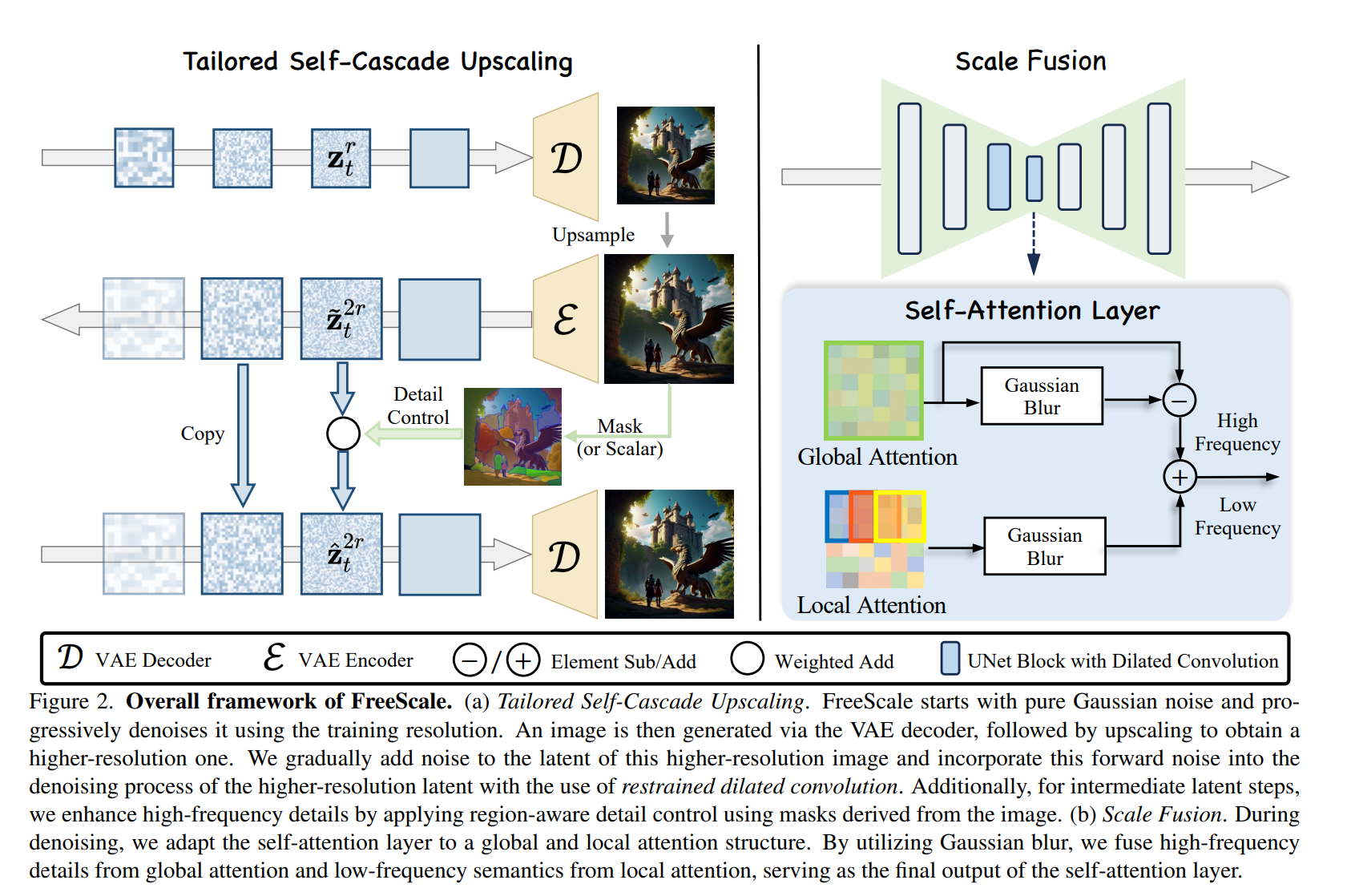
Tailored Self-Cascade Upscaling

Directly generating higher-resolution results will easily produce several repetitive objects, losing the reasonable visual structure that was originally good. To address this issue, we utilize a self-cascade upscaling framework from previous works [13, 14], which progressively increases the resolution of generated results: \[ \tilde{\mathbf{z}}_K^{2 r} \sim \mathcal{N}\left(\sqrt{\bar{\alpha}_K} \phi\left(\mathbf{z}_0^r\right), \sqrt{1-\bar{\alpha}_K} \mathbf{I}\right) \] where \(\tilde{\mathbf{z}}\) means the noised intermediate latent, \(r\) is the resolution level ( 1 represents original resolution, 2 represents the twice height and width), and \(\phi\) is an up sampling operation. In this way, the framework will generate a reasonable visual structure in low resolution and maintain the structure when generating higher-resolution results.

There are two options for \(\phi\) : directly up sampling in latent \((\phi(\mathbf{z})=\mathrm{UP}(\mathbf{z}))\) or up sampling in RGB space \((\phi(\mathbf{z})=\) \(\mathcal{E}(\operatorname{UP}(\mathcal{D}(\mathbf{z})))\), where \(\mathcal{E}\) and \(\mathcal{D}\) are the encoder and decoder of pre-trained VAE, respectively. Up sampling in RGB space is closer to human expectations but will add some blurs. We empirically observe that these blurs will hurt the video generation but help to suppress redundant over frequency information in the image generation. Therefore, we adopt up sampling in RGB space for higher-solution image generation and latent space up sampling in higher solution video generation.

Flexible Control for Detail Level

Add more detail from upscaled image during the initial noisy steps

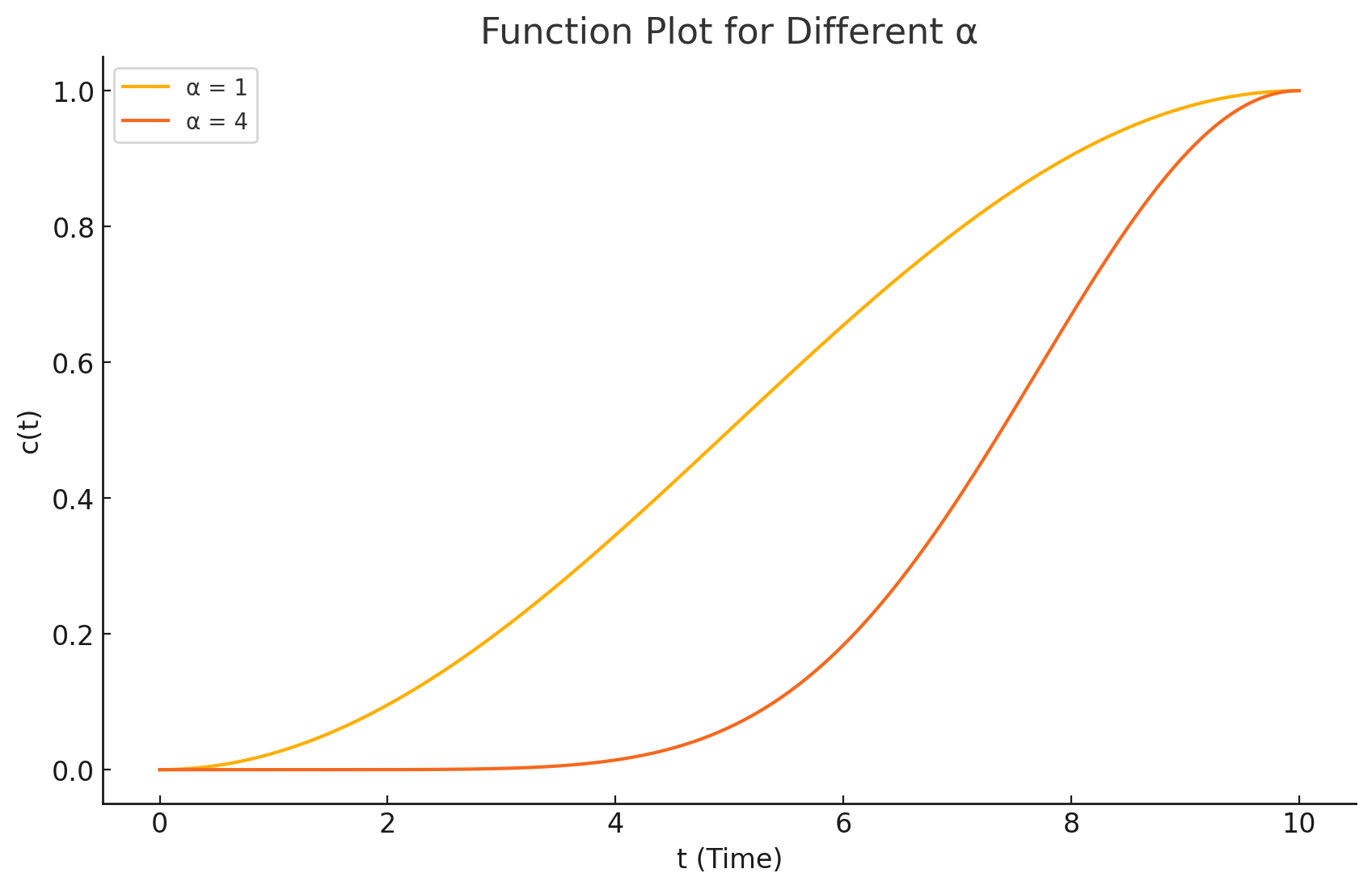
Flexible Control for Detail Level. Different from super resolution tasks, FreeScale will endlessly add more details as the resolution grows. This behavior will hurt the generation when all reasonable details are generated. To control the level of newly generated details, we modify \(p_\theta\left(\mathbf{z}_{t-1} \mid \mathbf{z}_t\right)\) to \(p_\theta\left(\mathbf{z}_{t-1} \mid \hat{\mathbf{z}}_t\right)\) with: \[ \hat{\mathbf{z}}_t^r=c \times \tilde{\mathbf{z}}_t^r+(1-c) \times \mathbf{z}_t^r \] where \(c=\left(\left(1+\cos \left(\frac{T-t}{T} \times \pi\right)\right) / 2\right)^\alpha\) is a scaled cosine decay factor with a scaling factor \(\alpha\).

Even in the same image, the detail level varies in different areas. To achieve more flexible control, \(\alpha\) can be a 2D-tensor and varies spatially. In this case, users can assign different values for different semantic areas according to \(\mathcal{D}\left(\mathbf{z}_0^r\right)\) calculated in the previous process already.

Restrained Dilated Convolution

ScaleCrafter emphasizes the limitations of the convolutional receptive field, while HiDiffusion focuses on feature duplication and redundancy in self-attention mechanisms. Currently, there is no evidence suggesting a direct connection or citation relationship between the two papers. Both provide complementary insights into addressing high-resolution generation challenges in diffusion models.

ScaleCrafter [18] observes that the primary cause of the object repetition issue is the limited convolutional receptive field and proposes dilated convolution to solve it. Given a hidden feature map \(\mathbf{h}\), a convolutional kernel \(\boldsymbol{k}\), and the the dilation operation \(\Phi_d(\cdot)\) with factor \(d\), the dilated convolution can be represented as: \[ f_k^d(\mathbf{h})=\mathbf{h} \circledast \Phi_d(\boldsymbol{k}),\left(\mathbf{h} \circledast \Phi_d(\boldsymbol{k})\right)(o)=\sum_{s+d \cdot t=p} \mathbf{h}(p) \cdot \boldsymbol{k}(q), \] where \(o, p\), and \(q\) are spatial locations used to index the feature or kernel. \(\circledast\) denotes convolution operation.

To avoid catastrophic quality decline, ScaleCrafter [18] only applies dilated convolution to some layers of UNet while still consisting of several up-blocks. However, we find that dilated convolution in the layers of up-blocks will bring many messy textures. Therefore, unlike previous works, we only apply dilated convolution in the layers of down-blocks and mid-blocks. In addition, the last few timesteps only render the details of results and the visual structure is almost fixed. Therefore, we use the original convolution in the last few timesteps.

Scale Fusion

global high pass + local low pass

Problem: Dilated convolution weakens the focus on local features, so it can gen 4x resolution images but can't generate 16x resolution images. DemoFusion [13] addresses this by using local patches to enhance local focus. However, although the local patch operation mitigates local repetition, it brings small object repetition globally.
Solution: we design Scale Fusion, which fuses information from different receptive scales to achieve a balanced enhancement of local and global details.
- Regarding global information extraction, we utilize global self-attention features. The reason is that the self-attention layer enhances the patch information based on similarity, making it easier for the subsequent cross-attention layer to aggregate semantics into a complete object. This can be formulated as:
\[ \begin{aligned} & \mathbf{h}_{\text {out }}^{\text {global }}=\operatorname{SelfAttention}\left(\mathbf{h}_{\text {in }}\right)=\operatorname{softmax}\left(\frac{Q K^T}{\sqrt{d \prime}}\right) V, \\ & \text { where } Q=L_Q\left(\mathbf{h}_{\text {in }}\right), K=L_K\left(\mathbf{h}_{\text {in }}\right), V=L_V\left(\mathbf{h}_{\text {in }}\right) . \end{aligned} \]
- In this formulation, query \(Q\), key \(K\), and value \(V\) are calculated from \(\mathbf{h}_{\text {in }}\) through the linear layer \(L\), and \(d \iota\) is a scaling coefficient for the self-attention. After that, the self-attention layer is independently applied to these local latent representations via \(\mathbf{h}_{\text {out, } \mathrm{n}}=\) Self-Attention \(\left(\mathbf{h}_{\mathrm{in}, \mathrm{n}}\right)\). And then \(\mathcal{H}_{\text {out }}^{\text {local }}=\left[\mathbf{h}_{\text {out }, 0} \cdots, \mathbf{h}_{\text {out }, \mathrm{n}} \cdots, \mathbf{h}_{\text {out, } \mathrm{N}}\right]\) is reconstructed to the original size with the overlapped parts averaged as \(\mathbf{h}_{\text {out }}^{\text {local }}=\mathcal{R}_{\text {local }}\left(\mathcal{H}_{\text {out }}^{\text {local }}\right)\), where \(\mathcal{R}_{\text {local }}\) denotes the reconstruction process.
- Regarding local information extraction, we follow previous works [ \(2,13,37\) ] by calculating self-attention locally to enhance the local focus. Specifically, we first apply a shifted crop sampling, \(\mathcal{S}_{\text {local }}(\cdot)\), to obtain a series of local latent representations before each self-attention layer, i.e., \(\mathcal{H}_{\mathrm{in}}^{\text {local }}=\mathcal{S}_{\text {local }}\left(\mathbf{h}_{\text {in }}\right)=\left[\mathbf{h}_{\text {in, } 0} \cdots, \mathbf{h}_{\text {in, } \mathrm{n}} \cdots, \mathbf{h}_{\text {in, } \mathrm{N}}\right], \mathbf{h}_{\text {in, } \mathrm{n}} \in\) \(\mathbb{R}^{c \times h \times w}\), where \(N=\left(\frac{(H-h)}{d_h}+1\right) \times\left(\frac{(W-w)}{d_w}+1\right)\), with \(d_h\) and \(d_w\) representing the vertical and horizontal stride, respectively. After that, the self-attention layer is independently applied to these local latent representations via \(\mathbf{h}_{\text {out, } \mathrm{n}}=\operatorname{SelfAttention}\left(\mathbf{h}_{\mathrm{in}, \mathrm{n}}\right)\). The resulting outputs \(\mathcal{H}_{\text {out }}^{\text {local }}=\left[\mathbf{h}_{\text {out }, 0} \cdots, \mathbf{h}_{\text {out, } \mathrm{n}} \cdots, \mathbf{h}_{\text {out, } \mathrm{N}}\right]\) are then mapped back to the original positions, with the overlapped parts averaged to form \(\mathbf{h}_{\text {out }}^{\text {local }}=\mathcal{R}_{\text {local }}\left(\mathcal{H}_{\text {out }}^{\text {local }}\right)\), where \(\mathcal{R}_{\text {local }}\) denotes the reconstruction process. While \(\mathbf{h}_{\text {out }}^{\text {local }}\) tends to produce better local results, it can bring unexpected small object repetition globally. These artifacts mainly arise from dispersed high-frequency signals, which will originally be gathered to the right area through global sampling. Therefore, we replace the high-frequency signals in the local representations with those from the global level \(\mathbf{h}_{\text {out }}^{\text {global }}\) :
\[ \mathbf{h}_{\text {out }}^{\text {fusion }}=\underbrace{\mathbf{h}_{\text {out }}^{\text {global }}-G\left(\mathbf{h}_{\text {out }}^{\text {global }}\right)}_{\text {high frequency }}+\underbrace{G\left(\mathbf{h}_{\text {out }}^{\text {local }}\right)}_{\text {low frequency }}, \]

where \(G\) is a low-pass filter implemented as a Gaussian blur, and \(\mathbf{h}_{\text {out }}^{\text {global }}-G\left(\mathbf{h}_{\text {out }}^{\text {global }}\right)\) acts as a high pass of \(\mathbf{h}_{\text {out }}^{\text {fusion }}\).

Experiments

Conclusion

ScaleCrafter emphasizes the limitations of the convolutional receptive field, while HiDiffusion focuses on feature duplication and redundancy in self-attention mechanisms. Currently, there is no evidence suggesting a direct connection or citation relationship between the two papers. Both provide complementary insights into addressing high-resolution generation challenges in diffusion models.

This paper is based on ScaleCrafter and developed some tricks.

This study introduces FreeScale, a tuning-free inference paradigm designed to enhance high-resolution generation capabilities in pre-trained diffusion models.

By leveraging multi-scale fusion and selective frequency extraction, FreeScale effectively addresses common issues in high resolution generation, such as repetitive patterns and quality degradation. Experimental results demonstrate the superiority of FreeScale in both image and video generation, surpassing existing methods in visual quality while also having significant advantages in inference time. Compared to prior approaches, FreeScale not only eliminates various forms of visual repetition but also ensures detail clarity and structural coherence in generated visuals. Eventually, FreeScale achieves unprecedented \(\mathbf{8 k}\)-resolution image generation.