SDEdit
Abstract
Guided image synthesis enables everyday users to create and edit photo-realistic images with minimum effort. The key challenge is balancing faithfulness to the user inputs (e.g., hand-drawn colored strokes) and realism of the synthesized images. Existing GAN-based methods attempt to achieve such balance using either conditional GANs or GAN inversions, which are challenging and often require additional training data or loss functions for individual applications. To address these issues, we introduce a new image synthesis and editing method, Stochastic Differential Editing (SDEdit), based on a diffusion model generative prior, which synthesizes realistic images by iteratively denoising through a stochastic differential equation (SDE).
Given an input image with user guide in a form of manipulating RGB pixels, SDEdit first adds noise to the input, then subsequently denoises the resulting image through the SDE prior to increase its realism. SDEdit does not require task-specific training or inversions and can naturally achieve the balance between realism and faithfulness. SDEdit outperforms state-of-the-art GAN-based methods by up to \(98.09 \%\) on realism and \(91.72 \%\) on overall satisfaction scores, according to a human perception study, on multiple tasks, including stroke-based image synthesis and editing as well as image compositing.
Introduction
The key intuition of SDEdit is to “hijack” the generative process of SDE-based generative models, as illustrated in Fig. 2. Given an input image with user guidance input, such as a stroke painting or an image with stroke edits, we can add a suitable amount of noise to smooth out undesirable artifacts and distortions (e.g., unnatural details at stroke pixels), while still preserving the overall structure of the input user guide. We then initialize the SDE with this noisy input, and progressively remove the noise to obtain a denoised result that is both realistic and faithful to the user guidance input (see Fig. 2).
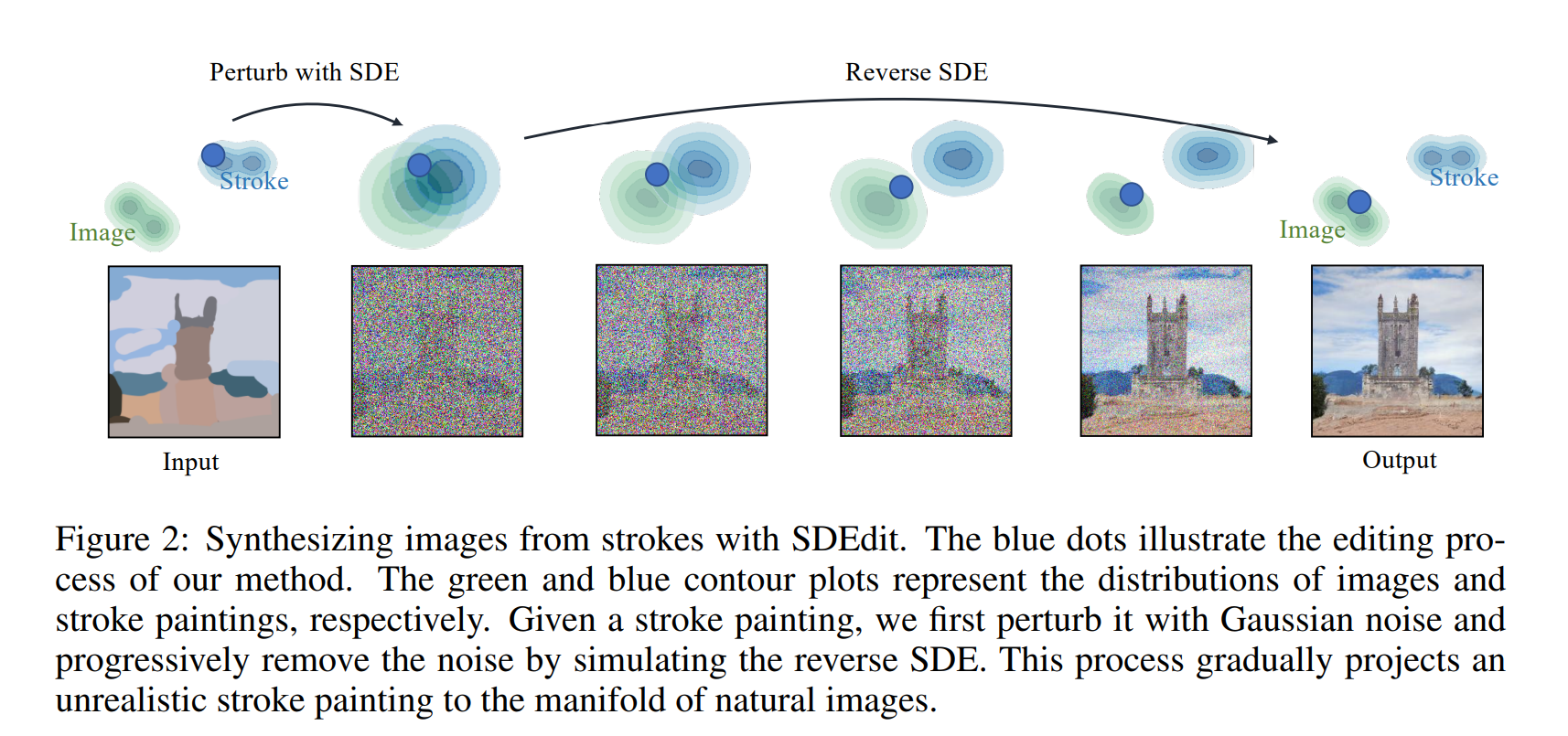
SDEdit naturally finds a trade-off between realism and faithfulness: when we add more Gaussian noise and run the SDE for longer, the synthesized images are more realistic but less faithful. We can use this observation to find the right balance between realism and faithfulness.
Background: Stochastic Differential Equations (SDEs)
we suppose that \(\mathbf{x}(0) \sim p_0=p_{\text {data }}\) represents a sample from the data distribution and that a forward SDE produces \(x(t)\) for \(t \in (0,1]\) via a Gaussian diffusion. Given \(x(0)\): \[ \mathbf{x}_t=\alpha_t \mathbf{x}_0 +\sigma_t \mathbf{z}, \quad \mathbf{z} \sim \mathcal{N}(\mathbf{0}, \boldsymbol{I}) \] Two types of SDE: Both VE and VP SDE transform the data distribution to random Gaussian noise as t goes from 0 to 1.
- Variance Exploding SDE (VE-SDE): \(\alpha(t)=1, t \in any\), \(\sigma(1) = large \,int\), \(\text { so that } p_1 \text { is close to } \mathcal{N}\left(\mathbf{0}, \sigma^{\mathbf{2}}(\mathbf{1}) \mathbf{I}\right)\)
- Variance Preserving (VP) SDE: \(\alpha^2(t)+\sigma^2(t)=1 \text { for all } t \text { with } \alpha(t) \rightarrow 0 \text { as } t \rightarrow 1\), so that \(p1 \sim N(0, I)\)
Image synthesis with VE-SDE. \[ \mathrm{d} \mathbf{x}(t)=\left[-\frac{\mathrm{d}\left[\sigma^2(t)\right]}{\mathrm{d} t} \nabla_{\mathbf{x}} \log p_t(\mathbf{x})\right] \mathrm{d} t+\sqrt{\frac{\mathrm{d}\left[\sigma^2(t)\right]}{\mathrm{d} t}} \mathrm{~d} \overline{\mathbf{w}} \] where \(\overline{w}\) is a wiener process or standard Brownian motion \[ d\overline{w} \sim N(0, dt) \] we use \(\boldsymbol{s}_\theta(\mathbf{x}(t), t)\) to approximate \(\nabla_{\mathbf{x}} \log p_t(\mathbf{x})\), if it can output the added noise, then it approximates well.
the SDE solution can be approximated with the Euler-Maruyama method; an update rule from (t + ∆t) to t is \[ \mathbf{x}(t)=\mathbf{x}(t+\Delta t)+\left(\sigma^2(t)-\sigma^2(t+\Delta t)\right) \boldsymbol{s}_{\boldsymbol{\theta}}(\mathbf{x}(t), t)+\sqrt{\sigma^2(t)-\sigma^2(t+\Delta t)} \mathbf{z} \] ==I think the equation might add a absolute under sqrt, for \(\sigma^2(t)-\sigma^2(t+\Delta t) < 0\)==
SDEdit

Setup: The user provides a full resolution image \(\mathbf{x}^{(g)}\) in a form of manipulating RGB pixels, which we call a "guide". The guide may contain different levels of details; a high-level guide contains only coarse colored strokes, a mid-level guide contains colored strokes on a real image, and a low-level guide contains image patches on a target image. We illustrate these guides in Fig. 1, which can be easily provided by non-experts. Our goal is to produce full resolution images with two desiderata:
Realism: The image should appear realistic (e.g., measured by humans or neural networks).
Faithfulness: The image should be similar to the guide x (g) (e.g., measured by L2 distance).
Procedure.
Our method, SDEdit, uses the fact that the reverse SDE can be solved not only from \(t_0=1\), but also from any intermediate time \(t_0 \in(0,1)\) - an approach not studied by previous SDE-based generative models. We need to find a proper initialization from our guides from which we can solve the reverse SDE to obtain desirable, realistic, and faithful images. For any given guide \(\mathbf{x}^{(g)}\), we define the SDEdit procedure as follows: \[ \text { Sample } \mathbf{x}^{(g)}\left(t_0\right) \sim \mathcal{N}\left(\mathbf{x}^{(g)} ; \sigma^2\left(t_0\right) \mathbf{I}\right) \text {, then produce } \mathbf{x}(0) \text { by iterating Equation } 4 . \] We use \(\operatorname{SDEdit}\left(\mathbf{x}^{(g)} ; t_0, \theta\right)\) to denote the above procedure. Essentially, SDEdit selects a particular time \(t_0\), add Gaussian noise of standard deviation \(\sigma^2\left(t_0\right)\) to the guide \(\mathbf{x}^{(g)}\) and then solves the corresponding reverse SDE at \(t=0\) to produce the synthesized \(\mathbf{x}(0)\).
Realism-faithfulness trade-off.
We note that for properly trained SDE models, there is a realism faithfulness trade-off when choosing different values of \(t_0\). To quantify realism, we adopt neural methods for comparing image distributions, such as the Kernel Inception Score (KID).
The realism-faithfulness trade-off can be interpreted from another angle. If the guide is far from any realistic images, then we must tolerate at least a certain level of deviation from the guide (non faithfulness) in order to produce a realistic image. This is illustrated in the following proposition.

Choice of \(t_{0}\)
- For reasonable guides: \(t_{0} \in [0.3, 0.6]\)
- If the guide is an white image with only white pixels, then even the closest “realistic” samples from the model distribution can be quite far, and we must sacrifice faithfulness for better realism by choosing a large \(t_{0}\)
In interactive settings (where user draws a sketch-based guide):
we can initialize \(t_{0} \in [0.3, 0.6]\), synthesize a candidate with SDEdit, and ask the user whether the sample should be more faithful or more realistic.
