Noise Schedule in Diffusion Models

iDDPM(DDPM)

1. get the \(\beta_t\), \(t \in [1, T]\)
2. Use \(\beta_t\) to create gaussion diffusion

guassion diffusion (cosine)

• \(\beta_t\)

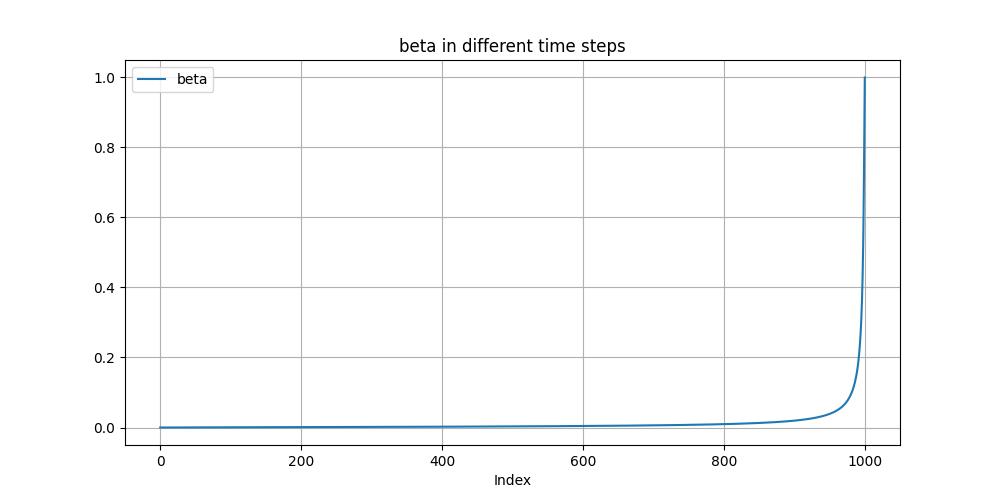
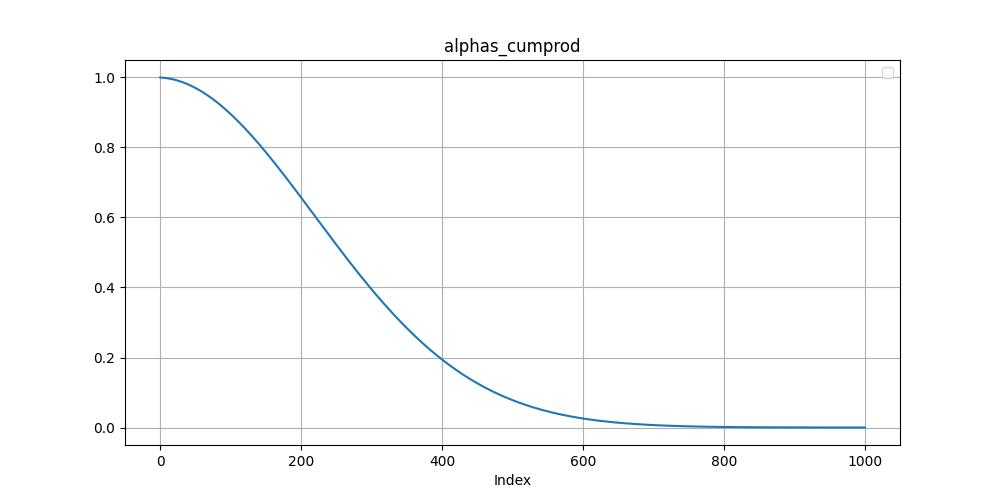
• \(\bar{\alpha}_t\) alphas_cumprod = np.cumprod(alphas, axis=0)

• Calculations for diffusion \(q\left(\mathbf{x}_t \mid \mathbf{x}_{0}\right)=\mathcal{N}\left( \sqrt{\bar{\alpha}_t} \mathbf{x}_{0}, (1-\bar{\alpha}_t) \mathbf{I}\right)\)

  In the code, although the model's output is \(\epsilon\), they transfrom it to the style of \(x_0\) \[ \begin{cases} x_t=\sqrt{\overline{\alpha_t}} x_0+\sqrt{1-\overline{\alpha_t}} \varepsilon_t \\ x_0 = \sqrt{\frac{1}{\bar{\alpha}_t}} x_t - \sqrt{\frac{1}{\bar{\alpha}_t}-1} \epsilon_t \end{cases} \]

• Calculations for diffusion \(q\left(\mathbf{x}_{t-1} \mid \mathbf{x}_{t}\right)=\mathcal{N}\left( \mu, \sigma^2 \right)\)

  sample \(x_{t-1}\) from \(x_t\) and predicted \(x_0\) \[ \mu = \frac{1}{\sqrt{\alpha}_t} \left(\mathbf{x}_t-\frac{1-\alpha_t}{\sqrt{1-\bar{\alpha}_t}} \boldsymbol{\epsilon}_t\right) \]

  \[ \sigma^2 = \frac{1-\bar{\alpha}_{t-1}}{1-\bar{\alpha}_t} \beta_t \]

  the variance has two choices in paper: \[ \sigma_t^2 min=\beta_t \]

  \[ \sigma_t^2 max=\frac{1-\bar{\alpha}_{t-1}}{1-\bar{\alpha}_t} \beta_t \]

  sample \(x_{t-1}\) from the prediction of \(x_0\) \[ \begin{cases} \mathbf{x}_{t-1}=\frac{1}{\sqrt{\alpha_t}}\left(\mathbf{x}_t-\frac{1-\alpha_t}{\sqrt{1-\bar{\alpha}_t}} \boldsymbol{\epsilon}_t\right)+\sigma_t \mathbf{z} \\ x_t=\sqrt{\overline{\alpha_t}} x_0+\sqrt{1-\overline{\alpha_t}} \varepsilon_t \rightarrow \varepsilon_t =\frac{x_t-\sqrt{\overline{\alpha_t}}x_0}{\sqrt{1-\overline{\alpha_t}}} \end{cases} \] Substituting the equation below into the equation above, we will obtain \(x_{t-1}\) from the prediction of \(x_0\) \[ \begin{aligned} & \mathbf{x}_{t-1}= \frac{1}{\sqrt{\alpha_t}} \big( \mathbf{x}_t- \frac{(1-{\alpha}_t)({\mathbf{x}}_t - \sqrt{\bar{\alpha}_t} \mathbf{x}_0) }{1-\overline{\alpha}_t} \big) +\sigma_t \mathbf{z} \\ & \mathbf{x}_{t-1}= \frac{1}{\sqrt{\alpha_t}} \left(\frac{\alpha_t - \bar{\alpha}_t}{1-\bar{\alpha}_t} \mathbf{x}_t + \frac{\sqrt{\bar{\alpha}_t}({1-{\alpha}_t}) }{1-\bar{\alpha}_t} \mathbf{x}_0 \right)+\sigma_t \mathbf{z} \\ & \mathbf{x}_{t-1}= \frac{\sqrt{\bar{\alpha}_{t-1}}({1-{\alpha}_t}) }{1-\bar{\alpha}_t}\mathbf{x}_0 + \frac{\sqrt{\alpha_t}\left(1-\bar{\alpha}_{t-1}\right)}{1-\bar{\alpha}_t} \mathbf{x}_t +\sigma_t \mathbf{z} \\ \end{aligned} \] and it can be simplified the coefficients \(coef1\) and \(coef2\) : \[ \mathbf{x}_{t-1} = coef1(\mathbf{x}_0) + coef2(\mathbf{x}_t) +\sigma_t \mathbf{z} \]
  

Illustration for DDPM and DDIM

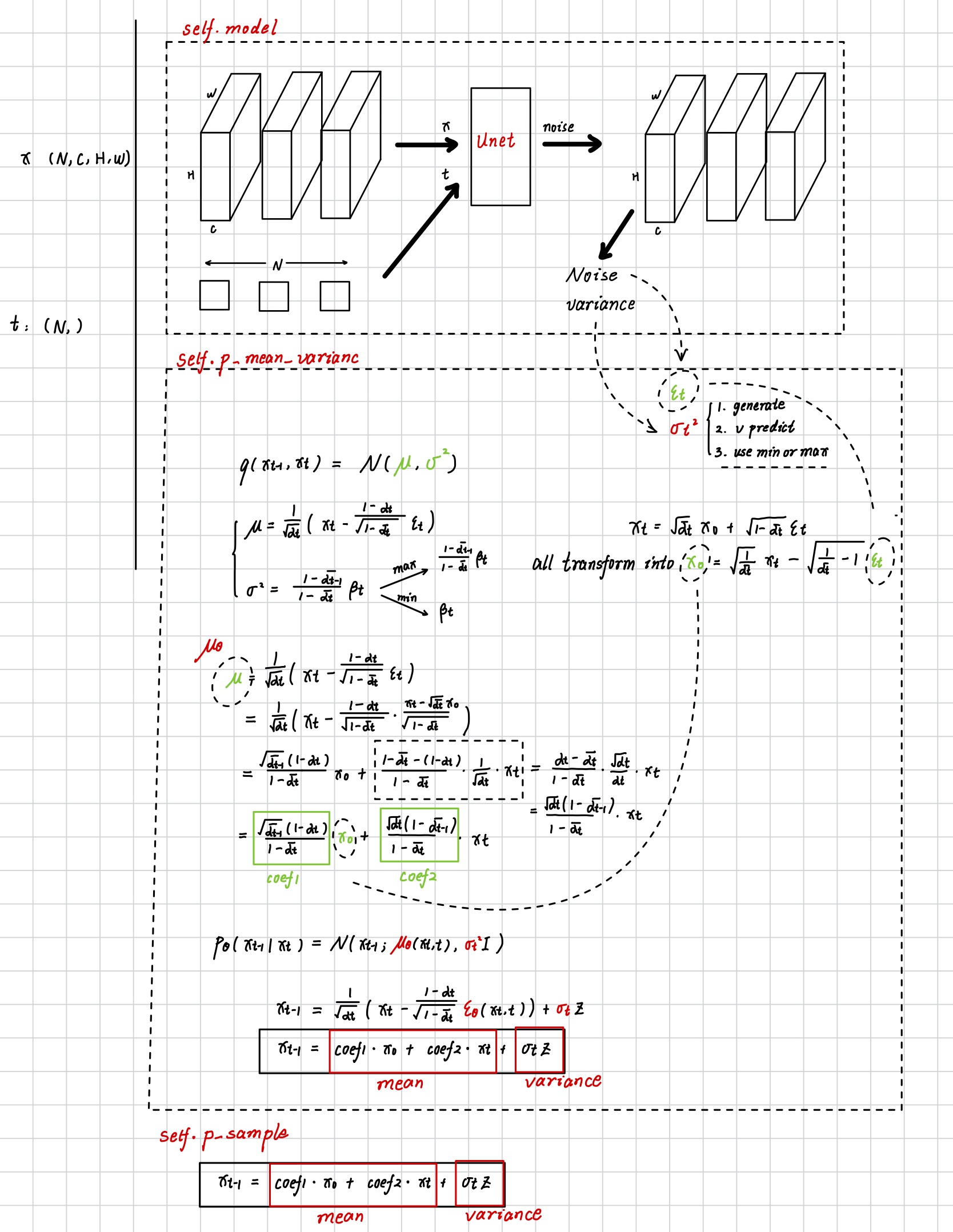
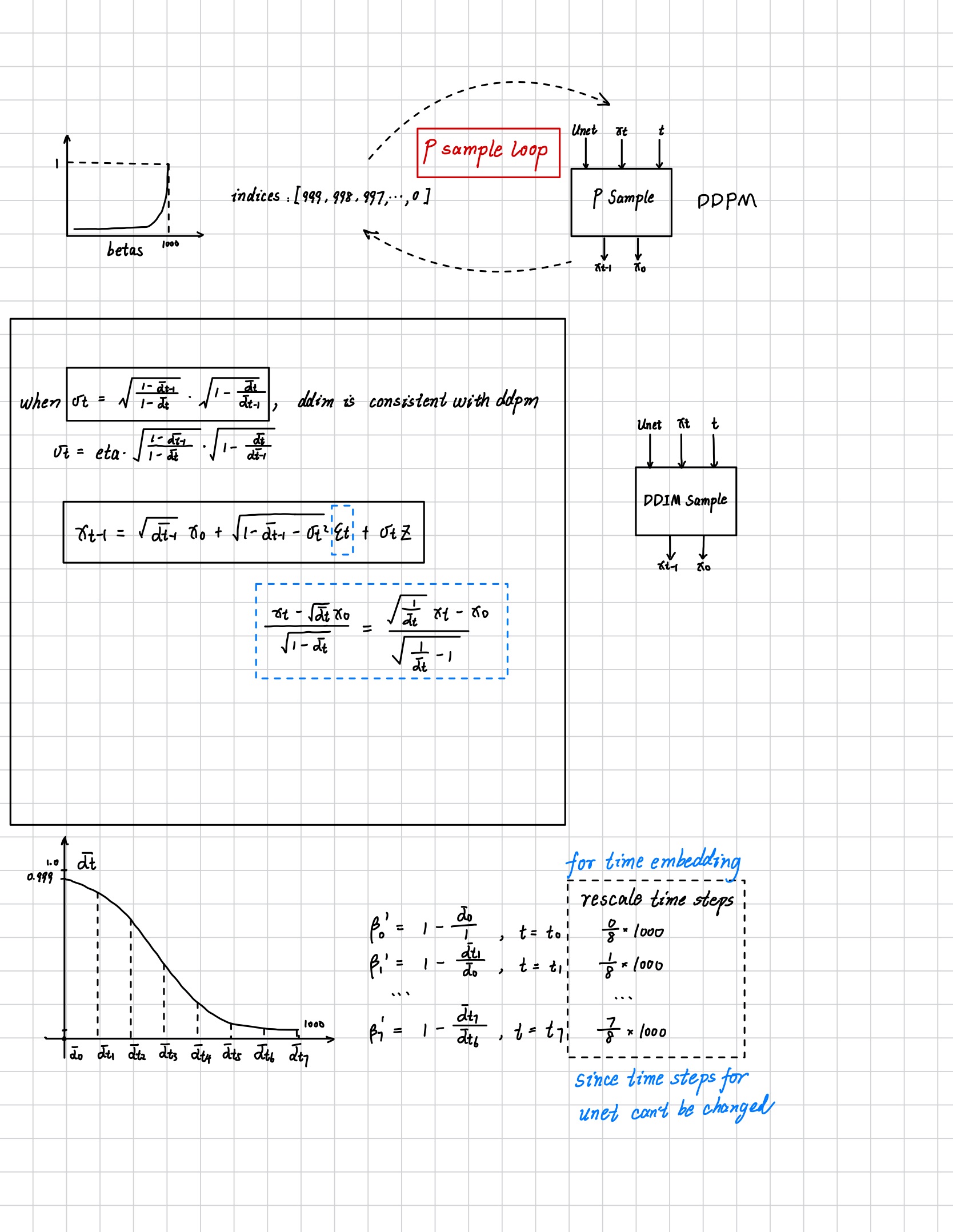
Illustration for Loss