ACE++
Abstract
Inspired by the input format for the inpainting task proposed by FLUX.1-Fill-dev, we improve the Long-context Condition Unit (LCU) introduced in ACE and extend this input paradigm to any editing and generation tasks.
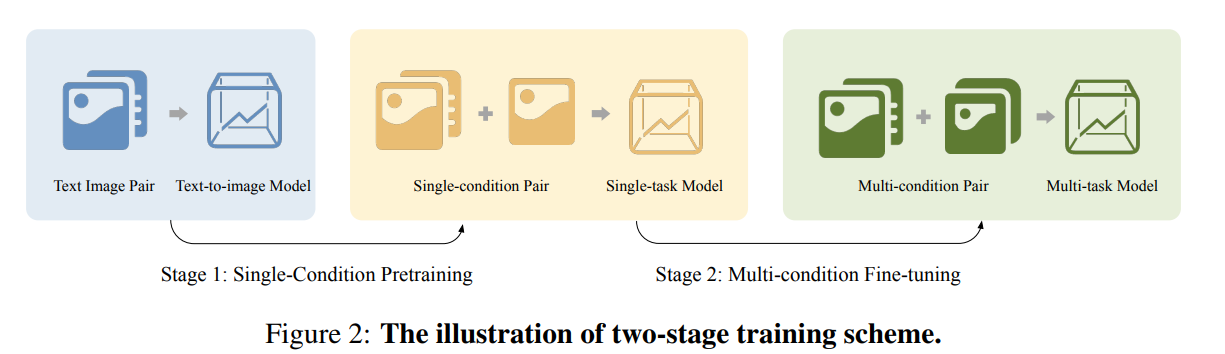
To take full advantage of image generative priors, we develop a two-stage training scheme to minimize the efforts of finetuning powerful text to-image diffusion models like FLUX.1-dev.
- we pre-train the model using task data with the 0-ref tasks from the text-to-image model
- we finetune the above model to support the general instructions using all tasks defined in ACE.
Introduction
In the community, many editing or reference generation methods are based on post-training of text to-image foundational models. For instance, FLUX.1-Fill-dev FLUX (2024) achieves inpainting task training by channel-wise concatenating the image to be edited, the area mask, and the noisy latent on the basis of the text-to-image model.
Inspired by this, we modified the input paradigm Long-context Condition Unit (LCU) introduced in ACE Han et al. (2024a) to reduce the substantial model adaptation costs brought by the introduction of multimodal inputs. By changing the conditional input for these tasks from sequence concatenation to channel dimension concatenation, we can effectively reduce the model adaptation costs. Furthermore, we propose an improved LCU input paradigm called LCU++ by extending this paradigm to arbitrary editing and reference generation tasks.
Based on the input definition of LCU++, we divide the entire training process into two stages.
- pre-training the model using task data with 0-ref tasks from the text-to-image model
- we fine-tune the above model to support the general instructions using all data collected in ACE Han et al.
Method
In addition, a noise unit is utilized to drive the generation process, which is constructed with the noisy latent \(X_t\) at timestep t and mask \(M_N\) . The overall formulation of the CU and the LCU is as follows: \[ \mathrm{CU}=\{T, V\}, \quad V=\left\{\left[I^1 ; M^1\right],\left[I^2 ; M^2\right], \ldots,\left[I^N ; M^N\right],\left[X_t ; M^N\right]\right\} \]
\[ \mathrm{LCU}=\left\{\left\{T_1, T_2, \ldots, T_m\right\},\left\{V_1, V_2, \ldots, V_m\right\}\right\} \]
Considering the generation tasks without reference image (denoted as 0-Ref tasks), the corresponding input format LCU0-ref can be expressed as follows: \[ \mathrm{LCU}_{0-\mathrm{ref}}=\{\{T\},\{V\}\}, \quad V_{0 \text {-ref }}=\left\{\left[I^{i n} ; M^{i n}\right],\left[X_t ; M^{i n}\right]\right\} \] where \(I^{in}\) and \(M^{in}\) is optional and represent the input image and mask.
Rather than sequence concatenation, We concatenate the conditional context and noise context in channel dimension, thereby mitigating the context perception disruption. The new format can be represented as: \[ \begin{aligned} \mathrm{LCU}^{++} & =\left\{\left\{T_1, T_2, \ldots, T_m\right\},\left\{V_1^{++}, V_2^{++}, \ldots, V_m^{++}\right\}\right\} \\ V^{++} & \left.=\left\{I^1 ; M^1 ; X_t^1\right],\left[I^2 ; M^2 ; X_t^2\right], \ldots,\left[I^N ; M^N ; X_t^N\right]\right\} \end{aligned} \] In each condition unit, the input image, mask, and noise are concatenated along the channel dimension to form the CU feature map. These CU feature maps are mapped to sequential tokens through the x-embed layer. Next, all CU tokens are concatenated to serve as the inputs of the transformer layer.
We design a novel and effective objective to optimize the training process. Given the input images \(I^i, i \in\{1,2, \ldots, N\}\) and the target output image \(I^o\), the noisy latent space \(\mathbf{x}_t=\left\{X_t^i\right\}, i \in\) \(\{1, \ldots, N\}\) can be constructed using a linear interpolation method from \(\left\{I^1, I^2, \ldots, I^{N-1}, I^o\right\}\). Here, \(I^N\) represents the sample that needs to be modified by the model. For editing tasks, this sample is the one to be edited. For reference generation tasks, this sample is an all-zero sample. The model is trained to predict the velocity \(\mathbf{u}_t=d \mathbf{x}_t / d_t\), guiding the sample \(\mathbf{x}_t\) towards the sample \(\mathbf{x}_1\). The training objective is to minimize the mean squared error between the predicted velocity \(\mathbf{v}_t\) and the ground truth velocity \(\mathbf{u}_t\), expressed as the loss function:
\[ \begin{aligned} \mathcal{L} & =\mathbb{E}_{t, \mathbf{x}_0, \mathbf{x}_1}\left\|\mathbf{v}_t-\mathbf{u}_t\right\|^2 . \\ & =\sum_{N-1}^{i=0} \mathbb{E}_{t, \mathbf{x}_0, \mathbf{x}_1}\left\|\mathbf{v}_t^i-\mathbf{u}_t^i\right\|^2+\mathbb{E}_{t, \mathbf{x}_0, \mathbf{x}_1}\left\|\mathbf{v}_t^N-\mathbf{u}_t^N\right\|^2 \\ & =\mathcal{L}_{\mathrm{ref}}+\mathcal{L}_{\mathrm{tar}} \end{aligned} \]
where \(\mathcal{L}_{\text {ref }}\) represents the reconstruct loss of the first \(\mathrm{N}-1\) reference samples and is equal to 0 in 0 -ref tasks. \(\mathcal{L}_{\text {tar }}\) represents the loss of the target sample being predicted. In this way, the model possesses context-aware generation capabilities.