Transfusion
TRANSFUSION: PREDICT THE NEXT TOKEN AND DIFFUSE IMAGES WITH ONE MULTI-MODAL MODEL
Abstract
We introduce Transfusion, a recipe for training a multi-modal model over discrete and continuous data. Transfusion combines the language modeling loss function (next token prediction) with diffusion to train a single transformer over mixed modality sequences. We pretrain multiple Transfusion models up to 7B parameters from scratch on a mixture of text and image data, establishing scaling laws with respect to a variety of uni- and cross-modal benchmarks. Our experiments show that Transfusion scales significantly better than quantizing images and training a language model over discrete image tokens. By introducing modality-specific encoding and decoding layers, we can further improve the performance of Transfusion models, and even compress each image to just 16 patches. We further demonstrate that scaling our Transfusion recipe to 7 B parameters and 2T multi-modal tokens produces a model that can generate images and text on a par with similar scale diffusion models and language models, reaping the benefits of both worlds.
Introduction
Many efforts have been made to combine these approaches, including
- extending a language model to use a diffusion model as a tool (act as an agent to call other component, LLaVA-Plus)
- grafting a pretrained diffusion model onto the language model (DreamLLM, Generating Images with Multimodal Language Models)
Alternatively, one can quantize the continuous modalities (VQ-VAE, VQ-GAN) and train a standard language model over discrete tokens, simplifying the model’s architecture at the cost of losing information.
In this work, we show it is possible to fully integrate both modalities, with no information loss, by training a single model to both predict discrete text tokens and diffuse continuous images.
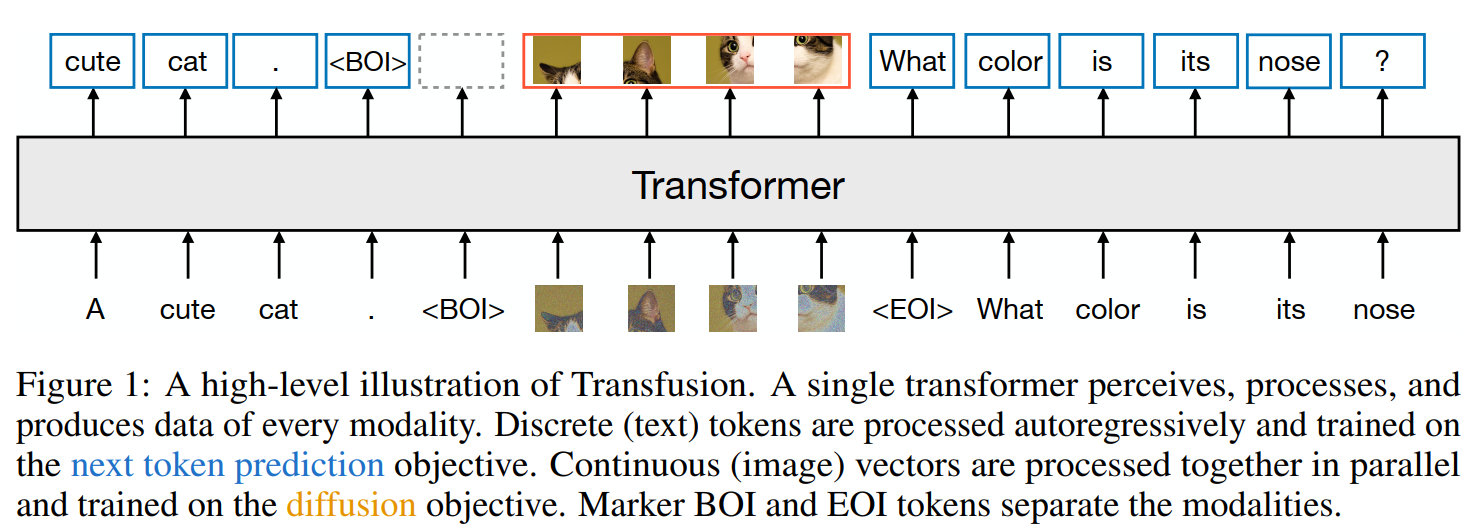
We introduce Transfusion, a recipe for training a model that can seamlessly generate discrete and continuous modalities. We demonstrate Transfusion by pretraining a transformer model on \(50 \%\) text and \(50 \%\) image data using a different objective for each modality: next token prediction for text and diffusion for images. The model is exposed to both modalities and loss functions at each training step. Standard embedding layers convert text tokens to vectors, while patchification layers represent each image as a sequence of patch vectors. We apply causal attention for text tokens and bidirectional attention for image patches. For inference, we introduce a decoding algorithm that combines the standard practices of text generation from language models and image generation from diffusion models. Figure 1 illustrates Transfusion.
In a controlled comparison with Chameleon's discretization approach (Chameleon Team, 2024), we show that Transfusion models scale better in every combination of modalities. In text-to-image generation, we find that Transfusion exceeds the Chameleon approach at less than a third of the compute, as measured by both FID and CLIP scores. When controlling for FLOPs, Transfusion achieves approximately \(2 \times\) lower FID scores than Chameleon models. We observe a similar trend in image-to-text generation, where Transfusion matches Chameleon at \(21.8 \%\) of the FLOPs. Surprisingly, Transfusion is also more efficient at learning text-to-text prediction, achieving perplexity parity on text tasks around \(50 \%\) to \(60 \%\) of Chameleon's FLOPs.
Ablation experiments reveal critical components and potential improvements for Transfusion. We observe that the intra-image bidirectional attention is important, and that replacing it with causal attention hurts text-to-image generation. We also find that adding U-Net down and up blocks to encode and decode images enables Transfusion to compress larger image patches with relatively small loss to performance, potentially decreasing the serving costs by up to \(64 \times\).
Finally, we demonstrate that Transfusion can generate images at similar quality to other diffusion models. We train from scratch a 7B transformer enhanced with U-Net down/up layers ( 0.27 B parameters) over 2T tokens: 1T text tokens, and approximately 5 epochs of 692 M images and their captions, amounting to another 1T patches/tokens. Figure 7 shows some generated images sampled from the model. On the GenEval (Ghosh et al., 2023) benchmark, our model outperforms other popular models such as DALL-E 2 and SDXL; unlike those image generation models, it can generate text, reaching the same level of performance as Llama 1 on text benchmarks. Our experiments thus show that Transfusion is a promising approach for training truly multi-modal models.
Background
Transfusion is a single model trained with two objectives: language modeling and diffusion. Each of these objectives represents the state of the art in discrete and continuous data modeling, respectively. This section briefly defines these objectives, as well as background on latent image representations.
Transfusion
Transfusion is a method for training a single unified model to understand and generate both discrete and continuous modalities. Our main innovation is demonstrating that we can use separate losses for different modalities - language modeling for text, diffusion for images - over shared data and parameters. Figure 1 illustrates Transfusion.
Data Representation We experiment with data spanning two modalities: discrete text and continuous images. Each text string is tokenized into a sequence of discrete tokens from a fixed vocabulary, where each token is represented as an integer. Each image is encoded as latent patches using a VAE (see §2.3), where each patch is represented as a continuous vector; the patches are sequenced left-to-right top-to-bottom to create a sequence of patch vectors from each image. For mixed-modal examples, we surround each image sequence with special beginning of image (BOI) and end of image (EOI) tokens before inserting it to the text sequence; thus, we arrive at a single sequence potentially containing both discrete elements (integers representing text tokens) and continuous elements (vectors representing image patches).
Model Architecture The vast majority of the model's parameters belong to a single transformer, which processes every sequence, regardless of modality. The transformer takes a sequence of high dimensional vectors in \(\mathbb{R}^d\) as input, and produces similar vectors as output. To convert our data into this space, we use lightweight modality-specific components with unshared parameters. For text, these are the embedding matrices, converting each input integer to vector space and each output vector into a discrete distribution over the vocabulary. For images, we experiment with two alternatives for compressing local windows of \(k \times k\) patch vectors into a single transformer vector (and vice versa): (1) a simple linear layer, and (2) up and down blocks of a U-Net (Nichol & Dhariwal, 2021; Saharia et al., 2022). Figure 3 illustrates the overall architecture.
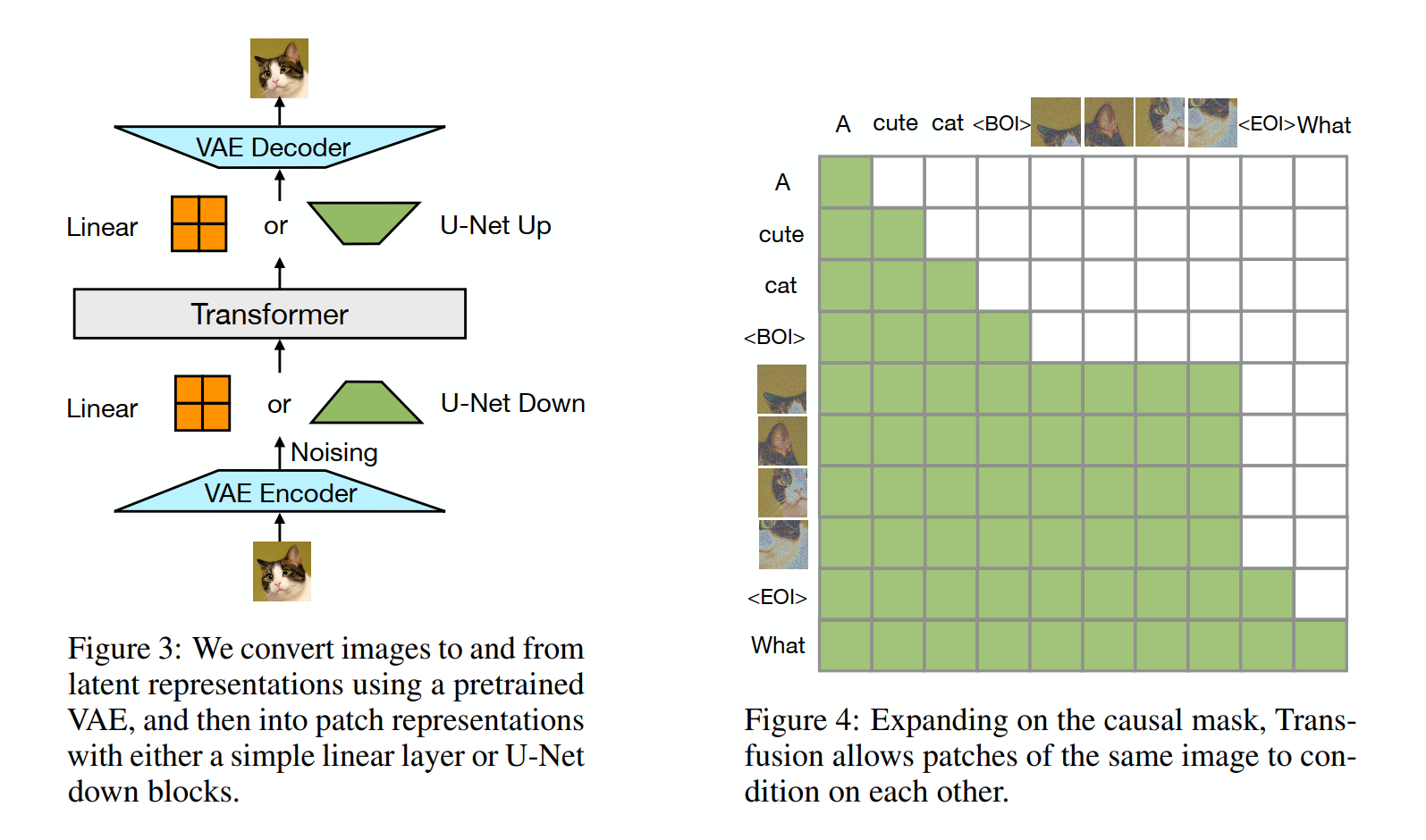
Transfusion Attention Language models typically use causal masking to efficiently compute the loss and gradients over an entire sequence in a single forward-backward pass without leaking information from future tokens. While text is naturally sequential, images are not, and are usually modeled with unrestricted (bidirectional) attention. Transfusion combines both attention patterns by applying causal attention to every element in the sequence, and bidirectional attention within the elements of each individual image. This allows every image patch to attend to every other patch within the same image, but only attend to text or patches of other images that appeared previously in the sequence. We find that enabling intra-image attention significantly boosts model performance (see \(\$ 4.3\) ). Figure 4 shows an example Transfusion attention mask.
Training Objective To train our model, we apply the language modeling objective \(\mathcal{L}_{\mathrm{LM}}\) to predictions of text tokens and the diffusion objective \(\mathcal{L}_{\text {DDPM }}\) to predictions of image patches. LM loss is computed per token, while diffusion loss is computed per image, which may span multiple elements (image patches) in the sequence. Specifically, we add noise \(\epsilon\) to each input latent image \(\mathbf{x}_0\) according to the diffusion process to produce \(\mathbf{x}_t\) before patchification, and then compute the image-level diffusion loss. 1 We combine the two losses by simply adding the losses computed over each modality with a balancing coefficient \(\lambda\) : \[ \mathcal{L}_{\text {Transfusion }}=\mathcal{L}_{\mathrm{LM}}+\lambda \cdot \mathcal{L}_{\mathrm{DDPM}} \]
This formulation is a specific instantiation of a broader idea: combining a discrete distribution loss with a continuous distribution loss to optimize the same model. We leave further exploration of this space, such as replacing diffusion with flow matching (Lipman et al., 2022)), to future work.
Inference Reflecting the training objective, our decoding algorithm also switches between two modes: LM and diffusion. In LM mode, we follow the standard practice of sampling token by token from the predicted distribution. When we sample a BOI token, the decoding algorithm switches to diffusion mode, where we follow the standard procedure of decoding from diffusion models. Specifically, we append a pure noise \(\mathbf{x}_T\) in the form of \(n\) image patches to the input sequence (depending on the desired image size), and denoise over \(T\) steps. At each step \(t\), we take the noise prediction and use it to produce \(\mathbf{x}_{t-1}\), which then overwrites \(\mathbf{x}_t\) in the sequence; i.e. the model always conditions on the last timestep of the noised image and cannot attend to previous timesteps. Once the diffusion process has ended, we append an EOI token to the predicted image, and switch back to LM mode. This algorithm enables the generation of any mixture of text and image modalities.
Experiments
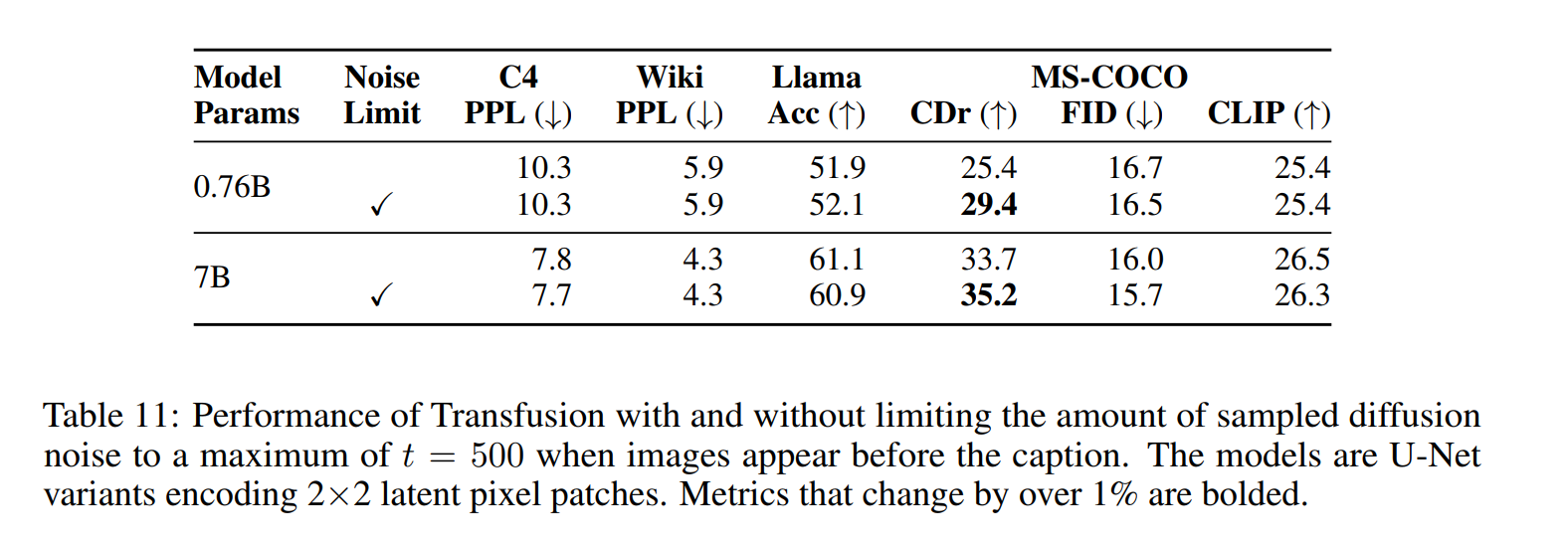
Our experiments order \(80 \%\) of image-caption pairs with the caption first, and the image conditioning on the caption, following the intuition that image generation may be a more data-hungry task than image understanding. The remaining \(20 \%\) of the pairs condition the caption on the image. However, these images are noised as part of the diffusion objective. We thus measure the effect of limiting the diffusion noise to a maximum of \(t=500\) (half of the noise schedule) in the \(20 \%\) of cases where images appear before their captions***. Table 11 shows that noise limiting significantly improves image captioning, as measure by CIDEr, while having a relatively small effect (less than \(1 \%\) ) on other benchmarks.
Image Editing

Our Transfusion models, which have been pretrained on text-text, image-text, and text-image data, perform well across these modality pairings. Can these models extend their capabilities to generate images based on other images? To investigate, we fine-tuned our 7 B model ( \(\$ 4.4\) ) using a dataset of only 8 k publicly available image editing examples, where each example consists of an input image, an edit prompt, and an output image. This approach, inspired by LIMA (Zhou et al., 2024), allows us to assess how well the model can generalize to image-to-image generation, a scenario not covered during pretraining. Manual examination of random examples from the EmuEdit test set (Sheynin et al., 2024), shown in Figure 6 and Appendix 4.5, reveals that our fine-tuned Transfusion model performs image edits as instructed. Despite the limitations of this experiment, the findings suggest that Transfusion models can indeed adapt to and generalize across new modality combinations. We leave further exploration of this promising direction to future research.
Conclusion
This work explores how to bridge the gap between the state of the art in discrete sequence modeling (next token prediction) and continuous media generation (diffusion). We propose a simple, yet previously unexplored solution: train a single joint model on two objectives, tying each modality to its preferred objective. Our experiments show that Transfusion scales efficiently, incurring little to no parameter sharing cost, while enabling the generation of any modality.